#Y1003. 启程(ongoing)
启程(ongoing)
题目描述
平面直角坐标系 中,现在散布着 个可看作点的码头,每个码头的坐标为 。
除了这些码头外,还有一个“中心调度点”。
从第 个码头到第 个码头()均有一条直线通道,于是共有 条通道。特别地,如果第 个码头重合,那么可以认为该通道覆盖了整个坐标系。
大卫哥站在 点,不禁想问:这些通道中,有多少条穿过了“中心调度点”,对于不同的 ,通道 和 被认为是不同的两个通道。
即:询问存在多少个有序点对 满足第 个点、第 个点和 点共线。
注意:保证对于 , 与第 个码头均不重合。
输入格式
第一行三个整数 ,意义如题述。
接下来 行,每行两个整数 ,表示每个码头的坐标。
输出格式
输出一行一个整数,即所有通道中穿过了“中心调度点”的数量。
样例
样例 1
3 0 1
1 3
2 5
3 4
2
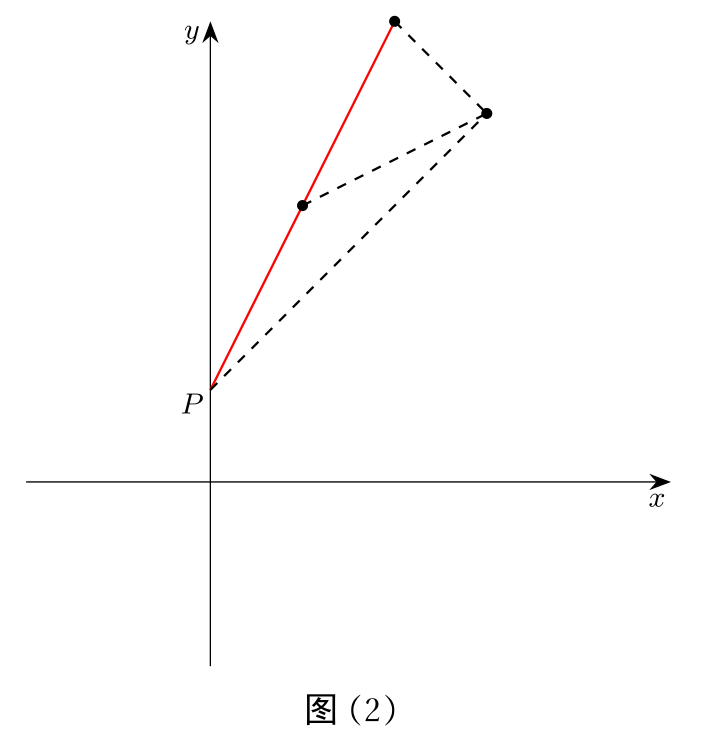
如图 (2) 描绘出了所有码头与通道,可以发现,仅有画红实线的 1 条通道穿过了“中心调度点”。于是被计算两次,答案为 2。
或者这样说明:数对 符合要求,所以答案为 2。
样例 2
见选手目录下的 ongoing/ongoing2.in 与 ongoing/ongoing2.ans。
该样例与测试数据 满足同样的约束条件。
数据范围
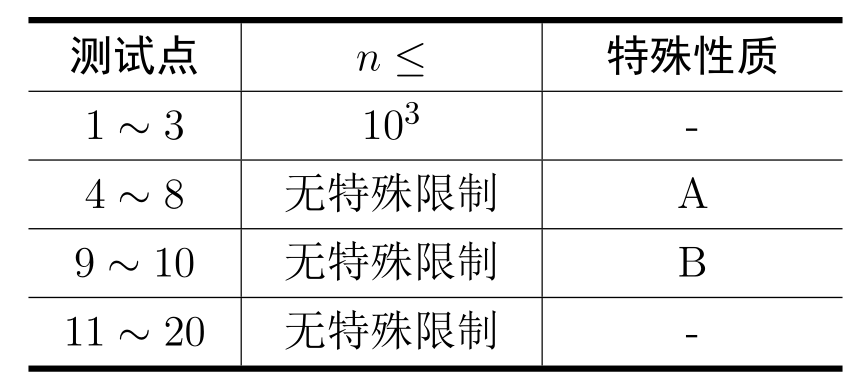
对于 的数据,有 , 且 。
相关
在下列比赛中:
