#925. Hongcow Builds A Nation
Hongcow Builds A Nation
Hongcow Builds A Nation
题面翻译
CF744A Hongcow Builds A Nation
给出一张 个点, 条边的无向图,其中有个点是警察局
一个稳定的图要满足以下条件:
- 无重边
- 无自环
- 每个连通块内最多只有一个警察局
你的任务是求最多还能加多少条边,使得加完边后的图还能是稳定的
输入格式
第一行三个整数,分别表示节点个数,无向边个数,和警察局个数
第二行 个正整数,表示警察局的编号
接下来 行,每行两个正整数 ,表示一条连接 的无向边
输出格式
一行一个整数,表示在保证图稳定的情况下,最多还能加的边数
数据范围
数据保证初始时给出的图是稳定的 感谢 @_Wolverine 提供的翻译
题目描述
Hongcow is ruler of the world. As ruler of the world, he wants to make it easier for people to travel by road within their own countries.
The world can be modeled as an undirected graph with nodes and edges. of the nodes are home to the governments of the countries that make up the world.
There is at most one edge connecting any two nodes and no edge connects a node to itself. Furthermore, for any two nodes corresponding to governments, there is no path between those two nodes. Any graph that satisfies all of these conditions is stable.
Hongcow wants to add as many edges as possible to the graph while keeping it stable. Determine the maximum number of edges Hongcow can add.
输入格式
The first line of input will contain three integers , and ( , , ) — the number of vertices and edges in the graph, and the number of vertices that are homes of the government.
The next line of input will contain integers ( ). These integers will be pairwise distinct and denote the nodes that are home to the governments in this world.
The following lines of input will contain two integers and ( ). This denotes an undirected edge between nodes and .
It is guaranteed that the graph described by the input is stable.
输出格式
Output a single integer, the maximum number of edges Hongcow can add to the graph while keeping it stable.
样例 #1
样例输入 #1
4 1 2
1 3
1 2
样例输出 #1
2
样例 #2
样例输入 #2
3 3 1
2
1 2
1 3
2 3
样例输出 #2
0
提示
For the first sample test, the graph looks like this:
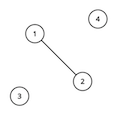 Vertices and are special. The optimal solution is to connect vertex to vertices and . This adds a total of edges. We cannot add any more edges, since vertices and cannot have any path between them.For the second sample test, the graph looks like this:
Vertices and are special. The optimal solution is to connect vertex to vertices and . This adds a total of edges. We cannot add any more edges, since vertices and cannot have any path between them.For the second sample test, the graph looks like this:
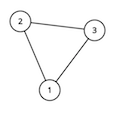 We cannot add any more edges to this graph. Note that we are not allowed to add self-loops, and the graph must be simple.
We cannot add any more edges to this graph. Note that we are not allowed to add self-loops, and the graph must be simple.
