Cyclic Components

题面翻译

题目描述

给定一张 $n$ 个点，$m$ 条边的无向图。保证无重边、无自环。在该图的所有连通块中，你需要找出环的个数。

无向图的环的定义如下：

原无向图中的一个子图被定义为环，当且仅当它的点集重新排序后可以满足如下条件：

• 第一个点与第二个点通过一条边相连接；
• 第二个点与第三个点通过一条边相连接；
• ……
• 最后一个点与第一个点通过一条边相连接。
• 所有的边都应当是不同的。
• 其边集不应当包含除了以上所述的边以外的任何边。

这样，我们就称这个子图（点 + 边）为环。

根据定义，一个环至少需要包含三个点，且边数与点数应当是相同的。

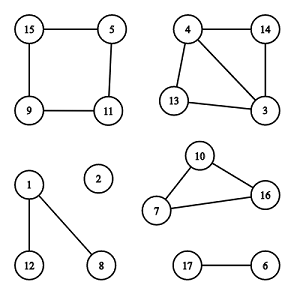
例如对于上图，共有 $6$ 个联通块，但只有 $[7,10,16]$ 和 $[5,11,9,15]$ 这两个联通块是环。

输入输出格式

输入格式：

第一行两个整数 $n$ 和 $m$ $(1 \le n \le 2 \cdot 10^5, 0 \le m \le 2 \cdot 10^5)$，分别表示图的点数和无向边数。

接下来 $m$ 行，第 $i$ 行包含两个整数 $v_i, u_i$ $(1 \le v_i, u_i \le n, u_i \not = v_i)$，表示第 $i$ 条边连接着 $v_i$ 与 $u_i$ 两点。

输出格式：

输出一行一个整数，表示环的个数。

说明

在第一个样例中，只有 $[3, 4, 5]$ 这个联通块是一个环。

第二个样例就对应着题目解释中的图片。

题目描述

You are given an undirected graph consisting of $n$ vertices and $m$ edges. Your task is to find the number of connected components which are cycles.

Here are some definitions of graph theory.

An undirected graph consists of two sets: set of nodes (called vertices) and set of edges. Each edge connects a pair of vertices. All edges are bidirectional (i.e. if a vertex $a$ is connected with a vertex $b$ , a vertex $b$ is also connected with a vertex $a$ ). An edge can't connect vertex with itself, there is at most one edge between a pair of vertices.

Two vertices $u$ and $v$ belong to the same connected component if and only if there is at least one path along edges connecting $u$ and $v$ .

A connected component is a cycle if and only if its vertices can be reordered in such a way that:

• the first vertex is connected with the second vertex by an edge,
• the second vertex is connected with the third vertex by an edge,
• ...
• the last vertex is connected with the first vertex by an edge,
• all the described edges of a cycle are distinct.

A cycle doesn't contain any other edges except described above. By definition any cycle contains three or more vertices.

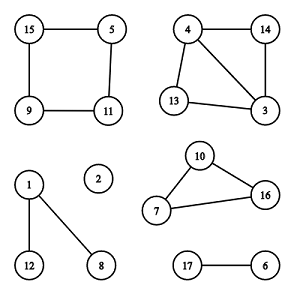There are $6$ connected components, $2$ of them are cycles: $[7, 10, 16]$ and $[5, 11, 9, 15]$ .

输入格式

The first line contains two integer numbers $n$ and $m$ ( $1 \le n \le 2 \cdot 10^5$ , $0 \le m \le 2 \cdot 10^5$ ) — number of vertices and edges.

The following $m$ lines contains edges: edge $i$ is given as a pair of vertices $v_i$ , $u_i$ ( $1 \le v_i, u_i \le n$ , $u_i \ne v_i$ ). There is no multiple edges in the given graph, i.e. for each pair ( $v_i, u_i$ ) there no other pairs ( $v_i, u_i$ ) and ( $u_i, v_i$ ) in the list of edges.

输出格式

Print one integer — the number of connected components which are also cycles.

样例 #1

样例输入 #1

5 4
1 2
3 4
5 4
3 5

样例输出 #1

1

样例 #2

样例输入 #2

17 15
1 8
1 12
5 11
11 9
9 15
15 5
4 13
3 13
4 3
10 16
7 10
16 7
14 3
14 4
17 6

样例输出 #2

2

提示

In the first example only component $[3, 4, 5]$ is also a cycle.

The illustration above corresponds to the second example.