#42. [NOIP2010-普及] 导弹拦截
[NOIP2010-普及] 导弹拦截
题目描述
经过 年的韬光养晦,某国研发出了一种新的导弹拦截系统,凡是与它的距离不超过其工作半径的导弹都能够被它成功拦截。当工作半径为 时,则能够拦截与它位置恰好相同的导弹。但该导弹拦截系统也存在这样的缺陷:每套系统每天只能设定一次工作半径。而当天的使用代价,就是所有系统工作半径的平方和。
某天,雷达捕捉到敌国的导弹来袭。由于该系统尚处于试验阶段,所以只有两套系统投入工作。如果现在的要求是拦截所有的导弹,请计算这一天的最小使用代价。
输入输出格式
输入格式:
第一行包含 个整数、、、,每两个整数之间用一个空格隔开,表示这两套导弹拦截系统的坐标分别为、。 第二行包含 个整数,表示有 颗导弹。接下来行,每行两个整数 ,中间用 一个空格隔开,表示一颗导弹的坐标。不同导弹的坐标可能相同。
输出格式:
一个整数,即当天的最小使用代价。
输入输出样例
输入样例#1:
0 0 10 0 2 -3 3 10 0
输出样例#1:
18
输入样例#2:
0 0 6 0 5 -4 -2 -2 3 4 0 6 -2 9 1
输出样例#2:
30
说明
两个点、之间距离的平方是。
两套系统工作半径的平方和,是指 分别取平方后再求和,即 。
【样例 说明】
样例中要拦截所有导弹,在满足最小使用代价的前提下,两套系统工作半径的平方分别为和。
【样例 说明】
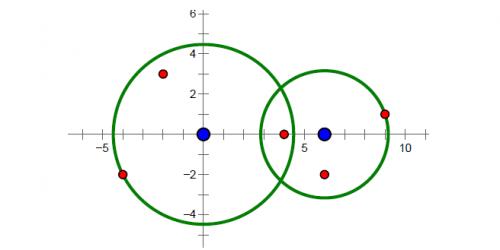
样例中的导弹拦截系统和导弹所在的位置如下图所示。要拦截所有导弹,在满足最小使用代价的前提下,两套系统工作半径的平方分别为 和。
【数据范围】
对于的数据,
对于的数据,
对于的数据,
对于的数据,
对于的数据,,且所有坐标分量的绝对值都不超过。
