题目描述

Kiana 最近沉迷于一款神奇的游戏无法自拔。

简单来说，这款游戏是在一个平面上进行的。

有一架弹弓位于 $(0,0)$ 处，每次 Kiana 可以用它向第一象限发射一只红色的小鸟，小鸟们的飞行轨迹均为形如 $y=ax^2+bx$ 的曲线，其中 $a,b$ 是Kiana 指定的参数，且必须满足 $a < 0$，$a,b$ 都是实数。

当小鸟落回地面（即 $x$ 轴）时，它就会瞬间消失。

在游戏的某个关卡里，平面的第一象限中有 $n$ 只绿色的小猪，其中第 $i$ 只小猪所在的坐标为 $\\left(x\_i,y\_i \\right)$。

如果某只小鸟的飞行轨迹经过了 $\\left( x\_i, y\_i \\right)$，那么第 $i$ 只小猪就会被消灭掉，同时小鸟将会沿着原先的轨迹继续飞行；

如果一只小鸟的飞行轨迹没有经过 $\\left( x\_i, y\_i \\right)$，那么这只小鸟飞行的全过程就不会对第 $i$ 只小猪产生任何影响。

例如，若两只小猪分别位于 $(1,3)$ 和 $(3,3)$，Kiana 可以选择发射一只飞行轨迹为 $y=-x^2+4x$ 的小鸟，这样两只小猪就会被这只小鸟一起消灭。

而这个游戏的目的，就是通过发射小鸟消灭所有的小猪。

这款神奇游戏的每个关卡对 Kiana来说都很难，所以Kiana还输入了一些神秘的指令，使得自己能更轻松地完成这个游戏。这些指令将在【输入格式】中详述。

假设这款游戏一共有 $T$ 个关卡，现在 Kiana想知道，对于每一个关卡，至少需要发射多少只小鸟才能消灭所有的小猪。由于她不会算，所以希望由你告诉她。

输入输出格式

输入格式：

第一行包含一个正整数 $T$，表示游戏的关卡总数。

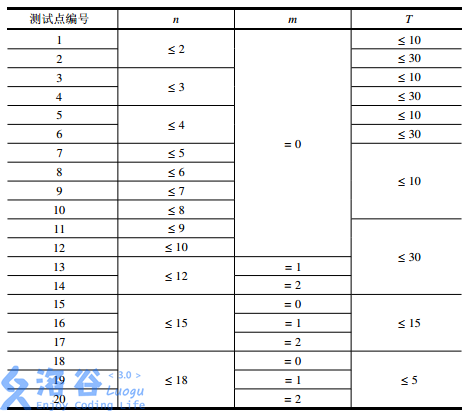
下面依次输入这 $T$ 个关卡的信息。每个关卡第一行包含两个非负整数 $n,m$，分别表示该关卡中的小猪数量和 Kiana 输入的神秘指令类型。接下来的 $n$ 行中，第 $i$ 行包含两个正实数 $x\_i,y\_i$，表示第 $i$ 只小猪坐标为 $(x\_i,y\_i)$。数据保证同一个关卡中不存在两只坐标完全相同的小猪。

如果 $m=0$，表示Kiana输入了一个没有任何作用的指令。

如果 $m=1$，则这个关卡将会满足：至多用 $\\lceil n/3 + 1 \\rceil$ 只小鸟即可消灭所有小猪。

如果 $m=2$，则这个关卡将会满足：一定存在一种最优解，其中有一只小鸟消灭了至少 $\\lfloor n/3 \\rfloor$ 只小猪。

保证 $1\\leq n \\leq 18$，$0\\leq m \\leq 2$，$0 < x\_i,y\_i < 10$，输入中的实数均保留到小数点后两位。

上文中，符号 $\\lceil c \\rceil$ 和 $\\lfloor c \\rfloor$ 分别表示对 $c$ 向上取整和向下取整，例如：$\\lceil 2.1 \\rceil = \\lceil 2.9 \\rceil = \\lceil 3.0 \\rceil = \\lfloor 3.0 \\rfloor = \\lfloor 3.1 \\rfloor = \\lfloor 3.9 \\rfloor = 3$。

输出格式：

对每个关卡依次输出一行答案。

输出的每一行包含一个正整数，表示相应的关卡中，消灭所有小猪最少需要的小鸟数量。

输入输出样例

输入样例#1： 复制

2 2 0 1.00 3.00 3.00 3.00 5 2 1.00 5.00 2.00 8.00 3.00 9.00 4.00 8.00 5.00 5.00

输出样例#1： 复制

1 1

输入样例#2： 复制

3 2 0 1.41 2.00 1.73 3.00 3 0 1.11 1.41 2.34 1.79 2.98 1.49 5 0 2.72 2.72 2.72 3.14 3.14 2.72 3.14 3.14 5.00 5.00

输出样例#2： 复制

2 2 3

输入样例#3： 复制

1 10 0 7.16 6.28 2.02 0.38 8.33 7.78 7.68 2.09 7.46 7.86 5.77 7.44 8.24 6.72 4.42 5.11 5.42 7.79 8.15 4.99

输出样例#3： 复制

6

说明

【样例解释1】

这组数据中一共有两个关卡。

第一个关卡与【问题描述】中的情形相同，$2$只小猪分别位于$(1.00,3.00)$和 $(3.00,3.00)$，只需发射一只飞行轨迹为$y = -x^2 + 4x$的小鸟即可消灭它们。

第二个关卡中有$5$只小猪，但经过观察我们可以发现它们的坐标都在抛物线 $y = -x^2 + 6x$上，故Kiana只需要发射一只小鸟即可消灭所有小猪。

【数据范围】