2018DLOI初中 第五题 矩阵乘法
说明
有一个 N 行 M 列的二维数组， 共 N*M 个格子， 每个格子都有一个价值。 第 1 行格子的价值从左往右是 1 至 M， 第 2 行格子的价值从左往右是 M+1 至 M+M， 最后 1 行格子的价值从左往右价值是(N-1)*M+1 至 N*M。 例如 N=3， M=4,那么该二维数组的价值如下所示：| 1 | 2 | 3 | 4 |
| 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 |
现在有 K 个操作， 每个操作是如下的两种情况之一：
1、 格式是 R X Y,表示行操作， 第 X 行的每个格子价值都乘上一个非负整数 Y。
2、 格式是 S X Y,表示列操作， 第 X 列的每个格子价值都乘上一个非负整数 Y。
当进行完 K 次操作之后， 你要输出所有格子的价值总和， 由于答案可能很大， 所以答案要模1000000007。
输入格式
第一行， 三个整数： N,M,K。接下来是 K 行， 每行的格式如题目所述。
输出格式
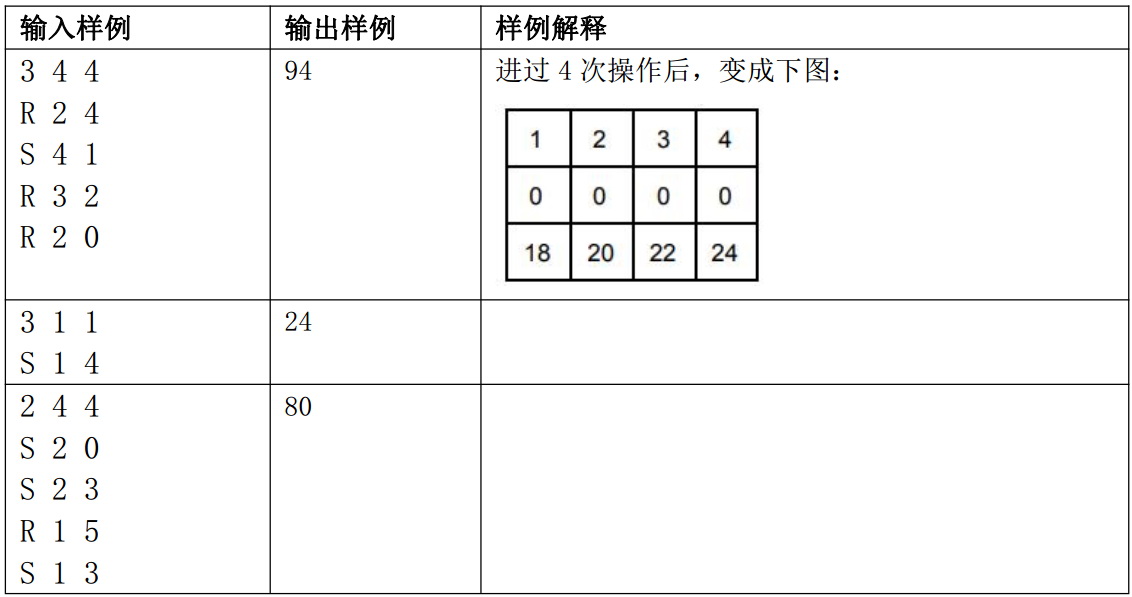
一个整数。样例
提示
【数据范围】
对于 50%的数据： 1 <= N,M <= 1000, 1 <= K <= 1000。 0 <= Y <= 1000000000
对于 100%的数据: 1<=N,M<=1000000， 1 <= K <= 1000。 0 <= Y <= 1000000000